GTSP Results

Computational Results for

A New Integer Programming Formulation of the Graphical Traveling Salesman Problem

Robert Carr, R. Ravi, Neil Simonetti

Abstract: In the Traveling Salesman Problem (TSP), a salesman wants to visit a set of cities and return home. There is a cost c_ij of traveling from city i to city j, which is the same in either direction for the Symmetric TSP. The objective is to visit each city exactly once, minimizing total travel costs. In the Graphical TSP, a city may be visited more than once, which may be necessary on a sparse graph. We present a new integer programming formulation for the Graphical TSP requiring only two classes of polynomial-sized constraints while addressing an open question proposed by Denis Naddef. We generalize one of these classes, and present promising preliminary computational results.

All formulations used subtour elimination constraints.
Constraint Descriptions can be found in our Springer Journal Article.

Even-Degree: Section 3.1
Parity: Section 4.1 (can be used in place of Even-Degree)
Spanning Tree: Section 4.2
Double-Degree: Section 5.2
z-Elimination: end of Section 6.1 (not valid with Steiner nodes)

Select an instance: Data sets and descriptions here.
Select a heading with 🌎 to view maps.
Best relaxation highlighted (where applicable).
First running time with Even-Degree constraints; second running time with Parity constraints. Running times on an Intel Xeon Gold 6126 processor at 2.6 GHz.

dakota3path (11 destinations) Integer Solution: 2682 miles, Subtour Relaxation: 2543 miles
Constraint Sets	With Steiner Nodes (not applicable)	Without Steiner Nodes \|V\|=11, \|E\|=12	Without Steiner Nodes and with z-Elimination
only Even-Degree or Parity		2543mi (0.01sec;0.01sec)	2543mi (0.01sec;0.01sec)
add Spanning Tree		2543mi (0.01sec;0.01sec)	2606.67mi (0.01sec;0.01sec)
add Double-Degree		2682mi (0.01sec;0.01sec)	2682mi (0.01sec;0.01sec)
add both		2682mi (0.01sec;0.01sec)	2682mi (0.01sec;0.01sec)

NFLcities (30 destinations) Integer Solution: 11524 miles, Subtour Relaxation: 11489 miles
Constraint Sets	With Steiner Nodes \|V\|=181, \|E\|=304	Without Steiner Nodes \|V\|=30, \|E\|=139	Without Steiner Nodes and with z-Elimination
only Even-Degree or Parity	11489mi (1.54sec;1.93sec)	11489mi (0.33sec;0.06sec)	11489mi (0.42sec;0.06sec)
add Spanning Tree	11489mi (11.59sec;11.94sec)	11489mi (1.43sec;2.91sec)	11489mi (1.39sec;1.43sec)
add Double-Degree	11489mi (1.87sec;1.74sec)	11489mi (0.25sec;0.07sec)	11489mi (0.41sec;0.06sec)
add both	11489mi (8.74sec;10.81sec)	11489mi (1.16sec;1.32sec)	11489mi (1.07sec;1.31sec)

NWcities (43 destinations) Integer Solution: 8119 miles, Subtour Relaxation: 8107 miles
Constraint Sets	With Steiner Nodes \|V\|=47, \|E\|=63	Without Steiner Nodes \|V\|=43, \|E\|=59	Without Steiner Nodes and with z-Elimination
only Even-Degree or Parity	8107mi (0.04sec;0.03sec)	8107mi (0.03sec;0.03sec)	8119mi (0.03sec;0.03sec)
add Spanning Tree	8107mi (0.35sec;0.07sec)	8107mi (0.40sec;0.07sec)	8119mi (0.05sec;0.05sec)
add Double-Degree	8111mi (0.04sec;0.03sec)	8111mi (0.04sec;0.03sec)	8119mi (0.04sec;0.03sec)
add both	8111mi (0.33sec;0.06sec)	8111mi (0.42sec;0.06sec)	8119mi (0.34sec;0.05sec)

CAPcities (49 destinations) Integer Solution: 14878 miles, Subtour Relaxation: 14844 miles
Constraint Sets	With Steiner Nodes \|V\|=181, \|E\|=301	Without Steiner Nodes \|V\|=49, \|E\|=199	Without Steiner Nodes and with z-Elimination
only Even-Degree or Parity	14844mi (1.93sec;2.25sec)	14844mi (0.73sec;0.98sec)	14844mi (0.71sec;0.86sec)
add Spanning Tree	14844mi (24.17sec;22.69sec)	14844mi (4.75sec;5.01sec)	14844mi (3.57sec;4.02sec)
add Double-Degree	14844mi (2.49sec;1.93sec)	14844mi (0.95sec;1.06sec)	14844mi (0.68sec;0.79sec)
add both	14844mi (25.01sec;20.84sec)	14844mi (4.65sec;3.78sec)	14844mi (3.79sec;3.62sec)

AtoJcities (101 destinations) Integer Solution: 17931 miles, Subtour Relaxation: 17669.5 miles
Constraint Sets	With Steiner Nodes \|V\|=196, \|E\|=326	Without Steiner Nodes \|V\|=101, \|E\|=289	Without Steiner Nodes and with z-Elimination
only Even-Degree or Parity	17669.5mi (4.13sec;2.95sec)	17669.5mi (2.61sec;2.55sec)	17702.5mi (3.25sec;3.43sec)
add Spanning Tree	17695.32mi (313.74sec;51.23sec)	17695.4mi (29.20sec;27.61sec)	17702.5mi (14.73sec;14.84sec)
add Double-Degree	17702.5mi (3.30sec;2.71sec)	17702.5mi (1.97sec;2.12sec)	17702.5mi (2.15sec;1.64sec)
add both	17702.5mi (23.19sec;43.63sec)	17702.5mi (11.88sec;15.00sec)	17702.5mi (14.89sec;12.87sec)

ESTcities (139 destinations) Integer Solution: 13251 miles, Subtour Relaxation: 13189.58 miles
Constraint Sets	With Steiner Nodes \|V\|=141, \|E\|=243	Without Steiner Nodes \|V\|=139, \|E\|=240	Without Steiner Nodes and with z-Elimination
only Even-Degree or Parity	13189.58mi (2.19sec;2.39sec)	13189.58mi (1.45sec;2.07sec)	13189.58mi (2.38sec;1.60sec)
add Spanning Tree	13189.58mi (27.57sec;27.53sec)	13189.58mi (34.28sec;30.37sec)	13189.58mi (28.87sec;18.87sec)
add Double-Degree	13197.08mi (2.70sec;2.65sec)	13197.08mi (2.32sec;2.69sec)	13197.08mi (3.42sec;2.85sec)
add both	13197.08mi (32.93sec;28.66sec)	13197.08mi (26.39sec;25.90sec)	13197.08mi (30.85sec;22.30sec)

MSAcities (145 destinations) Integer Solution: 22720 miles, Subtour Relaxation: 22577 miles
Constraint Sets	With Steiner Nodes \|V\|=208, \|E\|=348	Without Steiner Nodes \|V\|=145, \|E\|=317	Without Steiner Nodes and with z-Elimination
only Even-Degree or Parity	22577mi (4.79sec;5.42sec)	22577mi (3.83sec;3.71sec)	22580.75mi (4.81sec;4.68sec)
add Spanning Tree	22589mi (123.84sec;104.94sec)	22589mi (57.71sec;105.87sec)	22589mi (69.65sec;103.08sec)
add Double-Degree	22605.5mi (8.22sec;6.17sec)	22621.5mi (4.72sec;4.34sec)	22621.5mi (7.54sec;6.04sec)
add both	22605.5mi (65.58sec;56.60sec)	22621.5mi (64.86sec;69.64sec)	22621.5mi (310.82sec;57.24sec)

deg3cities (171 destinations) Integer Solution: 18737 miles, Subtour Relaxation: 18667 miles
Constraint Sets	With Steiner Nodes \|V\|=187, \|E\|=321	Without Steiner Nodes \|V\|=171, \|E\|=305	Without Steiner Nodes and with z-Elimination
only Even-Degree or Parity	18667mi (5.28sec;4.23sec)	18667mi (4.71sec;5.03sec)	18667mi (4.36sec;4.04sec)
add Spanning Tree	18667mi (445.84sec;60.59sec)	18667mi (68.32sec;44.16sec)	18667mi (50.21sec;59.75sec)
add Double-Degree	18667mi (6.08sec;5.61sec)	18667mi (6.31sec;6.06sec)	18667mi (5.36sec;5.76sec)
add both	18667mi (65.60sec;72.05sec)	18667mi (54.00sec;55.44sec)	18667mi (35.76sec;46.45sec)

NScities (174 destinations) Integer Solution: 22127 miles, Subtour Relaxation: 22033.5 miles
Constraint Sets	With Steiner Nodes \|V\|=203, \|E\|=341	Without Steiner Nodes \|V\|=174, \|E\|=324	Without Steiner Nodes and with z-Elimination
only Even-Degree or Parity	22033.5mi (3.24sec;3.38sec)	22033.5mi (3.80sec;3.12sec)	22037mi (4.65sec;6.23sec)
add Spanning Tree	22044.64mi (63.06sec;74.44sec)	22044.64mi (405.07sec;42.35sec)	22052.89mi (293.86sec;287.32sec)
add Double-Degree	22078.5mi (6.31sec;5.61sec)	22078.5mi (8.12sec;7.87sec)	22082mi (17.50sec;5.28sec)
add both	22078.5mi (68.83sec;60.51sec)	22078.5mi (54.75sec;47.89sec)	22082mi (66.23sec;33.55sec)

CtoWcities (182 destinations) Integer Solution: 24389 miles, Subtour Relaxation: 24238 miles
Constraint Sets	With Steiner Nodes \|V\|=212, \|E\|=353	Without Steiner Nodes \|V\|=182, \|E\|=358	Without Steiner Nodes and with z-Elimination
only Even-Degree or Parity	24238mi (4.86sec;5.23sec)	24238mi (4.85sec;4.50sec)	24251.75mi (14.35sec;5.09sec)
add Spanning Tree	24249.78mi (118.60sec;121.66sec)	24240.29mi (97.26sec;120.79sec)	24251.75mi (91.77sec;144.30sec)
add Double-Degree	24286mi (7.82sec;7.01sec)	24277.5mi (9.32sec;7.03sec)	24277.5mi (10.59sec;9.76sec)
add both	24286mi (107.28sec;752.15sec)	24277.5mi (104.68sec;94.79sec)	24277.5mi (94.43sec;115.80sec)

ALLcities (216 destinations) Integer Solution: 26410 miles, Subtour Relaxation: 26135.25 miles
Constraint Sets	With Steiner Nodes (not applicable)	Without Steiner Nodes \|V\|=216, \|E\|=358	Without Steiner Nodes and with z-Elimination
only Even-Degree or Parity		26135.25mi (4.51sec;5.53sec)	26135.25mi (14.91sec;13.39sec)
add Spanning Tree		26146.33mi (91.97sec;108.91sec)	26156.75mi (214.19sec;435.72sec)
add Double-Degree		26192.25mi (7.73sec;7.25sec)	26192.25mi (10.16sec;24.68sec)
add both		26192.25mi (105.37sec;125.16sec)	26192.25mi (265.28sec;85.32sec)

Maps for ALLcities (216 destinations)
Base Map This GTSP instance is interesting to study because, even though the only cut-edges and cut nodes are incident to and adjacent to leaf nodes (like Bellingham, Nogales, and Green Bay), the optimal solution has four edges of cost one adjacent to a single node (Kansas City).
Integer Solution 26410 miles
Subtour Relaxation (C-F-N) 26135.25 miles
Our Best Relaxation 26192.25 miles
Minimum Spanning Tree 20099 miles

WESTcanada (47 destinations) Integer Solution: 12022 km, Subtour Relaxation: 11997 km
Constraint Sets	With Steiner Nodes (not applicable)	Without Steiner Nodes \|V\|=47, \|E\|=73	Without Steiner Nodes and with z-Elimination
only Even-Degree or Parity		11997km (0.07sec;0.03sec)	11997km (0.08sec;0.03sec)
add Spanning Tree		11997km (0.08sec;0.04sec)	11997km (0.09sec;0.05sec)
add Double-Degree		11997km (0.06sec;0.03sec)	11997km (0.08sec;0.03sec)
add both		11997km (0.08sec;0.04sec)	11997km (0.09sec;0.05sec)

NScanada (56 destinations) Integer Solution: 14994 km, Subtour Relaxation: 14994 km
Constraint Sets	With Steiner Nodes \|V\|=75, \|E\|=108	Without Steiner Nodes \|V\|=56, \|E\|=84	Without Steiner Nodes and with z-Elimination
only Even-Degree or Parity	14994km (0.15sec;0.06sec)	14994km (0.09sec;0.04sec)	14994km (0.11sec;0.04sec)
add Spanning Tree	14994km (0.20sec;0.10sec)	14994km (0.11sec;0.06sec)	14994km (0.14sec;0.08sec)
add Double-Degree	14994km (0.15sec;0.06sec)	14994km (0.10sec;0.04sec)	14994km (0.12sec;0.05sec)
add both	14994km (0.20sec;0.11sec)	14994km (0.11sec;0.06sec)	14994km (0.14sec;0.08sec)

EASTcanada (65 destinations) Integer Solution: 15414 km, Subtour Relaxation: 15404 km
Constraint Sets	With Steiner Nodes (not applicable)	Without Steiner Nodes \|V\|=65, \|E\|=103	Without Steiner Nodes and with z-Elimination
only Even-Degree or Parity		15404km (0.14sec;0.06sec)	15404km (0.17sec;0.07sec)
add Spanning Tree		15404km (0.17sec;0.10sec)	15404km (0.22sec;0.13sec)
add Double-Degree		15414km (0.13sec;0.06sec)	15414km (0.17sec;0.08sec)
add both		15414km (0.18sec;0.11sec)	15414km (0.22sec;0.13sec)

DtoScanada (77 destinations) Integer Solution: 25066 km, Subtour Relaxation: 25042 km
Constraint Sets	With Steiner Nodes \|V\|=102, \|E\|=160	Without Steiner Nodes \|V\|=77, \|E\|=152	Without Steiner Nodes and with z-Elimination
only Even-Degree or Parity	25042km (0.31sec;0.15sec)	25042km (0.20sec;0.10sec)	25042km (0.24sec;0.11sec)
add Spanning Tree	25042km (0.40sec;0.24sec)	25042km (0.28sec;0.18sec)	25042km (0.33sec;0.22sec)
add Double-Degree	25042km (0.29sec;0.14sec)	25042km (0.20sec;0.11sec)	25042km (0.25sec;0.14sec)
add both	25042km (0.39sec;0.24sec)	25042km (0.28sec;0.18sec)	25042km (0.33sec;0.20sec)

deg3canada (90 destinations) Integer Solution: 19312 km, Subtour Relaxation: 19197 km
Constraint Sets	With Steiner Nodes \|V\|=93 \|E\|=149	Without Steiner Nodes \|V\|=90, \|E\|=146	Without Steiner Nodes and with z-Elimination
only Even-Degree or Parity	19197km (0.28sec;0.17sec)	19197km (0.26sec;0.14sec)	19197km (0.34sec;0.15sec)
add Spanning Tree	19197km (0.38sec;0.26sec)	19197km (0.36sec;0.25sec)	19197km (0.51sec;0.36sec)
add Double-Degree	19197km (0.27sec;0.15sec)	19197km (0.26sec;0.14sec)	19197km (0.34sec;0.19sec)
add both	19197km (0.38sec;0.29sec)	19197km (0.43sec;0.28sec)	19197km (0.46sec;0.25sec)

ALLcanada (112 destinations) Integer Solution: 27894 km, Subtour Relaxation: 27859 km
Constraint Sets	With Steiner Nodes (not applicable)	Without Steiner Nodes \|V\|=112, \|E\|=177	Without Steiner Nodes and with z-Elimination
only Even-Degree or Parity		27859km (0.46sec;0.28sec)	27859km (0.61sec;0.30sec)
add Spanning Tree		27859km (0.64sec;0.46sec)	27859km (0.94sec;0.60sec)
add Double-Degree		27869km (0.45sec;0.27sec)	27869km (0.55sec;0.38sec)
add both		27869km (0.63sec;0.47sec)	27869km (0.87sec;0.54sec)

Maps for ALLcanada (112 destinations)
Base Map This GTSP instance is interesting to study because it has a cut-edge (two, in fact) that separates the eastern cities from the western cities.
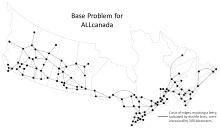Integer Solution 27894 kilometers
Subtour Relaxation (C-F-N) 27859 kilometers
Our Best Relaxation 27869 kilometers
Minimum Spanning Tree 18846 kilometers