1. Select a Trigonometric Calculation.
Choose a trigonometric function and angle
You need to select a function and angle before continuing.
2. Translate angle to degrees.
If you are not familiar with angles in radians, convert to degrees.
Angle in degrees = °
Since a full circle has 360° which is also 2π radians,
multiplying the radians value by the ratio 360/2π
(or 180/π in reduced from) will
give you the value of the angle in degrees.
3. Sketch the angle on the unit circle.
Click on the point on the unit circle corresponding to the angle.
Positive angles are drawn counter-clockwise from the positive x-axis.
Negative angles are drawn clockwise from the positive x-axis.
4. Determine the coordinates.
x coordinate =
y coordinate =
Note: for √2, type “r2”,
for √3, type “r3”,
for √4, just type “2”.
Thus, to enter √¾, type “r3/2”.
If the point is a simple compass point (north, south, east, or west), one of the coordinates
will be zero, and the other will be 1 or −1.
Otherwise, you may need to choose one of the two triangles below to place inside the
unit circle to help determine the coordinates (click on a triangle to see).
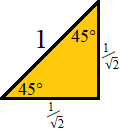
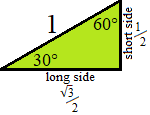Not that triangle.
This problem does not need a triangle.
5. Identify the trigonometric function in terms of x and y.
Each trigonometric function is a ratio involving x, y, or the distance
along the hypotenuse (which is always 1 on the unit circle).
Trigonometic ratio for =
 | cos θ = | adj | = | x | sin θ = | opp | = | y | ||
| hyp | 1 | hyp | 1 | |||||||
| tan θ = | opp | = | y | cot θ = | adj | = | x | |||
| adj | x | opp | y | |||||||
| sec θ = | hyp | = | 1 | csc θ = | hyp | = | 1 | |||
| adj | x | opp | y | |||||||
6. Final calculation.
Use the trigonometric ratio with the coordinates to calculate (and simplify) the final answer.
Final calculation for
() =
For √2, type “r2”.
Type “undefined” if you need to divide by zero.
| ( | a | ) | × c | When confronted by a compound fraction, you can simplify it by multiplying the top and bottom of the large fraction by the common denominator of the small fractions. |
| c | ||||
| ( | b | ) | × c | |
| c | ||||
7. Select a new problem at step 1.